Table of Contents
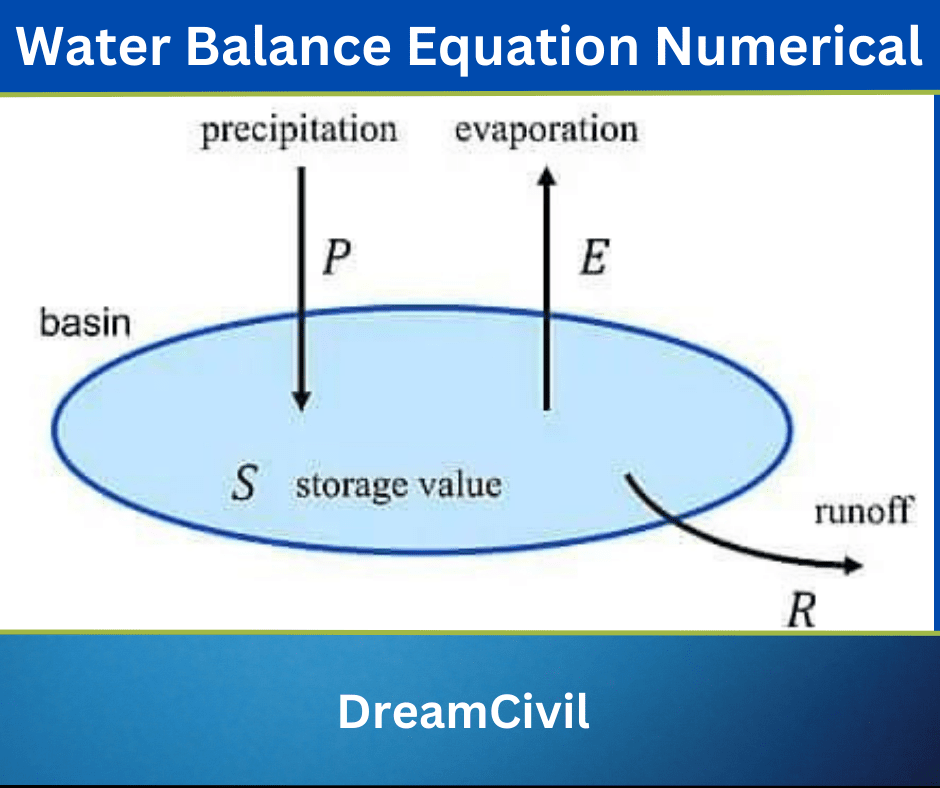
The water balance equation is the statement of the law of conservation of mass.
It is also called the continuity equation or conservation equation. In other words, it is the balance of the input and output of water within a given area taking into account net changes in storage.
Water Balance Equation Numerical are easy to solve, you need to do some of the noted below:
It can be defined by the following relationships.
Mass inflow – Mass outflow = Change in Inflow storage
If the density of inflow and outflow is the same,
Then,
Volume Inflow – Volume Outflow = Change in storage
Here, the main source of inflow is precipitation and outflows are surface runoff, evaporation, transpiration, interception, etc.
The relationship between rainfall and runoff is a very complex phenomenon as the parameters involved in the relationships are not very accurately determinable. Various components of water balance within the basin.
Before jumping on numerical we need to know the formula to be used in the Water Balance Equation Numerical.
General water budget equation in hydrology for time internal Δt.
P-(R+G+E+T)= ΔS
Where,
P = Precipitation
R = Surface runoff
G = Net groundwater flows out of the catchment
E = Evaporation
T = Transpiration
ΔS = Change in storage
All the terms in the equation have the dimensions of volume. Alternatively, these terms can also be expressed in the unit of depth, e.g. m, cm, mm.
a. To convert depth to volume, multiply depth by catchment area.
b. To convert flow rate to volume, multiply flow rate by time duration.
c. To convert volume to depth, divide the volume by catchment area.
In the case of other inflow besides precipitation, the water balance equation is
(P+I)-(R+G+E+T)= ΔS
I = other inflow
For the long term, e.g. annual water balance, change in storage is zero. In such a case, the general water balance equation is,
Precipitation – Runoff = Evapouration
1. Water Balance Equation Numerical
1. A river each had a flood wave passing through it. At a given instant the storage of water in the reach was estimated as 15.5 ha.m. What would be the storage in the reach after an interval of 3 hours if the average inflow and outflow during the time period are 14.2 m3/s and 10.6 m3/s respectively?
Solution:
Initial Storage= 15.5 ha.m = 15.5 x104 m3
Inflow rate= 14.2 m3/s
Inflow volume in 3 hours= 14.2 x 3x 60x 60 = 153360 m3
Outflow rate= 10.6 m3/s
Outflow volume in 3 hours= 10.6 x 3x 60x 60 = 114480 m3
Final Storage=?
From the water budget equation,
Inflow – Outflow= Change in storage
Inflow – Outflow= Final storage – Initial Storage
153360 – 114480 = Final storage – 15.5 x 104
Final Storage = 38880 + 15.5 x 104
= 193880 m3
2. Estimate the constant rate of withdrawal from a 1375 ha reservoir in a month of 30 days during which the reservoir level dropped by 0.75 m in spite of an average inflow into the reservoir of 0.5 million m3/day. During the month the average seepage loss from the reservoir was 2.5 cm, the total precipitation was 18.5 cm and the total evaporation was 9.5 cm.
Solution:
Reservoir area= 1375 ha = 1375 x104 m2
Inflow into the reservoir= 0.5×106 m3/day
Inflow volume in a month= 0.5×106 x 30 = 15×106 m3
Inflow in terms of depth(I)= 15 x 106/ (1375×104) = 1.091 m
Change in storage (ds)= 0.75 m
Seepage Loss(G) = 2.5cm =0.025m
Precipitation(P) = 18.5 cm= 0.185m
Evapouration= 9.5 cm = 0.095 m
Withdrawal (Q) =?
Writing water balance equation
(P+I)-(Q+G+E) = ds
(0.185+1.091)-(Q+0.025+0.095)=0.75
Q= 0.406m for a month
Rate of Withdrawal = 0.406x1375x104/(30x24x60x60)
= 2.15 m3/s
3. A catchment area of 140 Km2 received 120cm of rainfall in a year. At the outlet of the catchment, the flow in the stream draining the catchment was found to have an average rate of 2 m3/s for 3 months, 3m3/s for 6 months, and 5 m3/s for 3 months. Calculate the runoff coefficient of the catchment.
If the afforestation of the catchment reduced the runoff coefficient to 0.5, what is the increase in the abstraction from precipitation due to infiltration, evaporation, and transpiration, for the same annual rainfall of 120 cm?
Solution,
a. Catchment area = 140 Km2
Rainfall= 120 cm = 1.2 m
Rainfall in terms of volume (R)= 1.2 x140x106 =168×106 m3
Starting from January, Runoff = 2 m3/s for 3 months (90 days), 3 m3/s for 6 months (183 days), and 5 m3/s for 3 months (92 days)
Total runoff volume(Q)= 2x24x60x60x90+3x24x60x60x183+ 5x24x60x60x92 = 1.0273x 108 m3
Runoff coefficient (C)=?
C= Q/R= 1.0273x 108/ 168X106 = 0.61
b. Runoff coefficient (C1)=0.5
Rainfall(R)= 120 cm = 1.2 m
Increase in abstraction=?
C1= Q/R
Runoff= C1 x Rainfall = 0.15×1.2= 0.6m
Abstraction = Rainfall – Runoff
=1.2-0.6 = 0.6 x 140×106 = 84×106 m3
Abstraction in case = Rainfall – Runoff = 168 x 106 – 1.0273 x 108 = 84×106 m3
Increase in abstraction= 84×106– 65.27×106
= 18.73 x106 m3
4. The catchment area of the reservoir is 10.5 km2. Uniform precipitation of 0.5 cm/h for 2h was observed on a particular day. 50% of the runoff reached the reservoir.
A canal carrying a flow of 1 m3/s is taken from the reservoir. The rate of evaporation was 0.7 mm/hr/m2. Assuming seepage loss to be 50% of evaporation loss, find the change in reservoir level for 8 hours in the next if the water spread of the reservoir was 0.45 km2.
Solution:
The catchment area of the reservoir (A) = 10.5 Km2
Precipitation for 2h = 0.5×2 = 1cm = 0.01m
Volume of precipitation as inflow (I)= 50% of PxA = 0.5X0.001X10.5X106 = 52500 m3
Canal discharge (Q) = 1m3/s
Outflow volume for 8h (O) = 1x8x3600 = 28800 m3
Rate of evaporation (Er) = 0.7 mm/hr/m2 = 0.7/1000 m/hr/m2
Water spread of the reservoir (a) = 0.45 km2
Evapouration loss for 8h (E) = (Erxax8) = 0.7/1000 x 0.45×106 x 8 = 2520 m3
Seepage loss (S) = 0.5E = 0.5 x 2520 = 1260 m3
Change in reservoir level (dh) =?
Water Balance Equation,
I-(O+E+S) = dh
dh= 52500-(28800+2520+1260)
= 19920 m3
dh in terms of depth unit is given by,
dh/a = 19920/(0.45×106)
= 0.0443 m
dh/a = 44.3 m
| Read Also: Low E Glass |