Table of Contents
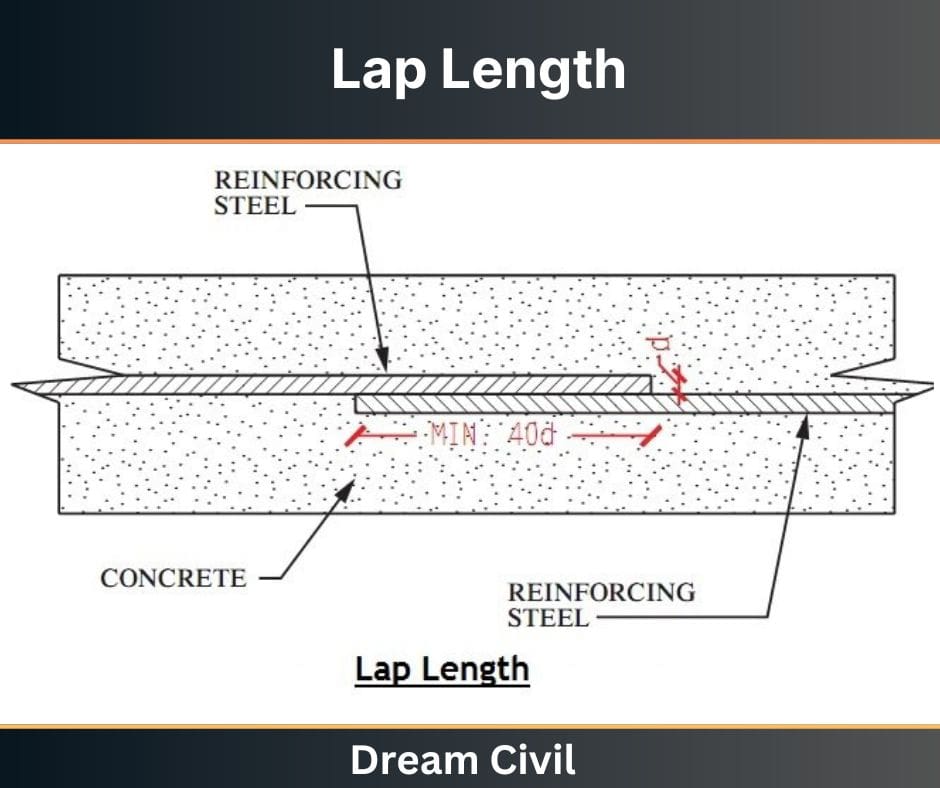
Lap length can be defined as the length provided to allow the overlapping of two reinforcement bars, thereby ensuring the safe and efficient load transfer from one bar to another.
When the reinforcement bars are placed, the length of a single reinforcement bar may not be sufficient.
In such a case, the required design length is achieved by overlapping two bars.
The lap length is thus provided to allow such lapping of the reinforcement bars side by side.
In other words, the overlap length between the two reinforcement bars is the lap length.
Lap length may also be provided when the diameter of the reinforcement bar has to be changed along the length, particularly during the reinforcement of columns.
Lapping the reinforcement bars side by side to obtain the desired design length is known as lapping.
The primary objective of providing the lap is to ensure the efficient transfer of axial force from the terminating bar to the new connected bar along the same line of action in the junction.
1. Overview
It is a general practice to manufacture the reinforcement steel bars in 12m lengths to ensure ease in transportation and handling.
However, larger beams, columns, and slabs may be required during the construction of reinforced concrete structures.
The reinforcement bars must be overlapped to get the desired length in such a case.
Usually, such overlapping of bars is done where the magnitude of the bending stress is the least.
When the two reinforcement bars have an equal diameter, the lap length can be calculated using the following formula:
Lap Length = 50 x D
Where,
D = diameter of the reinforcement bars
In case the diameters of the reinforcement bars are not equal, then the lap length is calculated using the bar’s value with a smaller diameter.
a. Lap Length in Tension
For the lap length in tension, the following formula can be used for calculating the lap length, including the anchorage value of the hooks,
1. For flexural tension, Lap length = L x d or 30 x d (The greater value among the two values calculated is taken.)
2. For direct tension, Lap length = 2 x L x d or 30 x d (The greater value among the two values calculated is taken.)
Where,
L = development length
In such a case, the straight lapping length of the reinforcement bars must be greater than 200 mm or 15 x d.
b. Lap Length in Compression
For the lap length in compression, the value of the lap length can be taken as the same as that of the development length.
However, the lap length cannot be less than 24 x d.
2. Importance of Providing Lap Length
The lap length is necessary for reinforced concrete structures to transfer tensile and compressive loads from one reinforcement bar to another by means of shear or skin friction.
The absence of lap length may disrupt the load transfer mechanism and lead to the failure of the entire structure.
Also, when the lap length is inadequate, the reinforcement bars may split, forming cracks in the concrete.
Thus, the lap length is necessary for reinforced concrete structures.
3. General Rules for Lap Length Determination
1. For the reinforcement bars with different diameters, the lap length must be calculated using the diameter of the smaller bar.
2. Staggering manner must be adopted for the lapping of the bars. When lapping is done, the laps should be given at a different level. This is done to prevent buckling.
3. The spacing of the stirrups must be done closely. Generally, when the Lapping is done, the strength of the concrete members decreases; thus, more stirrups must be provided to account for this.
4. Splicing one bar at a time must be done for lap splicing in case a bundle of reinforcement bars is required. Afterward, the staggering of each bar within it must be done.
4. Lap Length of Columns, Slabs & Beams
a. Lap Length of Columns
The codal provision for calculating the lap length of columns in a reinforced concrete structure is given in CL. 26.5.3 of IS 456:200.
According to this code, the diameter of the bars must not be less than 12mm.
The number of longitudinal bars provided in a rectangular column must be equal to or greater than four and equal to or greater than 6 in a circular column.
The spacing of such longitudinal bars should be lesser than 300mm when measured along the periphery of the column.
The lap length of columns can be calculated using the following formula,
Lap Length of Column = 45 x d
where;
d = diameter of the bar
b. Lap Length of Slabs
The codal provision for calculating the lap length of slabs in reinforced concrete structures is given in CL. 26.5.1 of IS 456:200.
According to this code, the reinforcement bars’ diameter must be less than one-eighth of the total slab thickness.
The lap length of slabs can be calculated using the following formula,
Lap Length of Slab = 60 x d
c. Lap Length of Beams
The codal provision for calculating the lap length of beams in reinforced concrete structures is given in CL. 26.5.2 of IS 456:200.
According to this code, side reinforcement bars must be provided if the depth of the beam’s web is greater than 75 cm.
In such a case, the area of the reinforcement bars used must be greater than 0.1 percent of the total area of the web.
The reinforcement bars must be equally distributed on both faces of the beam such that the spacing is not greater than 300 mm or the thickness of the web, whichever has a lesser value.
In beams, the transverse reinforcements must be provided to lie around the exterior tension and compression bars.
In T-beams and I-beams, such reinforcement shall pass around longitudinal bars close to the flange’s outer face.
The lap length of beams can be calculated using the following formula,
Lap Length of Beams = 60 x d
5. Numerical Examples
Q. Determine the lap length for two bars with a diameter of 40mm.
Solution,
When the two bars have the same diameter, the lap length can be calculated as,
Lap Length = 50 x d = 50 x 40 = 2000 mm = 2 m
Q. Determine the lap length for two bars in which the diameter of one bar is 25mm and another of diameter 40mm.
Solution,
When two bars have a different diameter, the smaller diameter must be used i.e.
Lap Length = 50 x d = 50 x 25 = 1250 mm = 12.5 m
Q. Determine the lap length for the beam, slab (Take the diameter of bar = 12 mm), and the lap length for the column (Take the diameter of bar = 24 mm).
Solution,
i. Lap Length of beam = 60 x d = 60 x 12 mm = 720 mm
ii. Lap Length of slab = 60 x d = 60 x 12 mm =720 mm
iii. Lap Length of column = 45 x d = 45 x 24 mm = 1080 mm
Q. Determine the lap length for the following:
i. Nominal Mix of 1:2:4, if the diameter of the bar is 20 mm.
Lap Length for 1:2:4 concrete mix = 40 x D = 40 x 20 mm = 800 mm
ii. Nominal Mix of 1:1.5:3 for the column if the diameter of the bar is 20 mm.
Lap Length for 1:1.5:3 concrete mix for column = 45 x D = 45 x 20 mm= 900 mm
iii. Nominal Mix of 1:1.5:3 for beam if the diameter of the bar is 20 mm.
Lap Length for 1:1.5:3 concrete mix for beam = 60 x D = 60 x 20 mm = 1200 mm
iv. Nominal Mix of 1:1.5:3 for the slab if the diameter of the bar is 20 mm.
Lap Length for 1:1.5:3 concrete mix for slab = 60 x D = 60 x 20 mm = 1200 mm
Q. Determine the lap length for flexural tension provided that the development length is 120mm and the diameter of the bar is 12 mm.
Solution,
For flexural tension,
Lap length = L x d or 30 x d (The greater value among the two values calculated is taken.)
= 120 x 12 or 30 x 12
= 1440 mm or 360 mm
Hence, the lap length is 1440 mm (since the greater value must be taken.)
6. Lapping Zones for Beams and Columns
a. Lapping Zone for Columns
Let us consider a column as shown in Fig below.
Let L be the length of the column under consideration.
The tension zone is present at a distance of L/4 from either end of the column. In such a zone, lapping must not be provided as this zone is subjected to tension.
At the central portion of the column, the bending moment is equal to zero, implying that the column’s mid-portion is subjected to the least stress.
Due to this reason, it is desirable to provide the lapping at this section of the column.
Thus, the stresses can be easily transferred from one reinforcement bar to another efficiently and smoothly in the mid-section of the column.

Figure: Lap Zone of Column
| Read More: Bar Bending Schedule |
b. Lapping Zone for Beams
In the case of a beam, the upper portion (top part) of the beam is subjected to compression, while the lower portion (bottom part) of the beam is subjected to both compression and tension.
Due to this reason, the uppermost reinforcement bar in the beam must be provided at the left side of the mid-span of the beam.
Since the beam is not subjected to the negative moment at the mid-section, thus it is desirable to provide lapping in this section.
On the other hand, for the bottom reinforcement, it is desirable to provide the lapping at the end sections of the beam.
The lapping can also be provided at a distance of L/4 from the face of the column, but it must be noted that it is not the mid-point of the beam.
It must also be noted that the lapping must not be provided at the joints.
7. Difference Between Lap Length and Development Length
| S.N. | Lap Length | Development Length |
| 1 | It refers to two reinforcement bars overlapping to achieve the desired design length. | It refers to the length necessary for transferring the stress imposed on the concrete member. |
| 2 | Lapping is done in reinforced concrete structures to achieve the required design length of the reinforcement bars. | Development length is necessary to achieve the bond strength between the concrete and the embedded reinforcement bar. |
8. References1. Content Filter & Authenticity Checking Team, Dream Civil International (Our team checks every content & detail to maintain quality.) |
| Read More: Prismatic Compass |

