Table of Contents
In this article, we will discuss the stability of slopes numerical.
In geotechnical engineering, the term slope commonly refers to a soil mass with its surface inclined to the horizontal, and there exist both natural and man-made slopes.
Natural slopes are those that exist in nature and are formed by natural causes. Such slopes exist in hilly areas. The sides of cuttings, the slopes of embankments constructed for roads, railway lines, canals, etc, and the slopes of earth dams constructed for storing water are examples of manmade slopes.

The failure of an earth slope occurs when a large mass of soil slides or slips along with a planet or a curved surface involving a downward and outward movement of the soil mass away from the sloping surface.
The surface along which the soil mass when the failure of an earth slope occurs is known as the critical surface of failure. It is evident that the failure of an earth slope occurs when the forces
to slide are greater than those tending to restore or stabilize the soil mass critical surface of failure.
1. Formulas
| Sn= C / FcγH |
Where,
γ = Unit weight of soil
H = Height of slope
C = Unit Ultimate Cohesion
a. Cohesionless Soil
i. Dry Soil:
The factor of safety against sliding is given as:
| FS = τf / τ |
Where,
τf = Shear Strength of Soil
τ = Shear Stress
ii. Submerged Condition
a). For partially submerged:
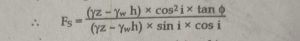 |
b). For Fully Submerged (z=h)
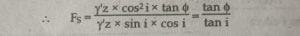 |
Where,
h= Depth of water
z= Depth of Slope
γ’ = Submerged unit weight of soil
Φ = Angle of internal friction
iii. Seepage Condition
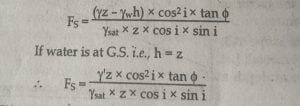 |
b. Cohesive Soil (c-Φ soil)
| FS = τf / τ |
| Fs = C+ σ tanΦ / τ |
2. Stability of Slopes Numerical
Here are a few important Stability of Slopes Numerical :
1. Calculate the factor of safety with respect to the cohesion of a clay slope laid at 1 in 2 to a height of 10 m, if the angle of internal friction Φ = 10º, c= 25 KN/m3, and γ = 19 KN/m2. What will be the critical height of the slope in this soil?
Solution:
Given that;
Φ = 10º
c= 25 KN/m3
γ = 19 KN/m2
H = 10 m
and, tani= 1/2
i = 26.5º
for Φ = 10º and i = 26.5º from the chart
| Sn= C / FcγH |
Fc = C/γHSn
Fc = 25 / 19x 0.064×10
Fc = 2.06
Again,
Hc = C/γSn
Hc = 25 / 19 x 0.64
Hc = 20.6 m
2. Calculate the safe height for an embankment rising 70º to the horizontal and to be made with clayey soil having a unit weight of 2.1 gm/c.c, Φ=15º, and cohesion of 0.2 kg/cm2. Take the factor of safety as 2.5.
Solution:
Since the factor of safety given in the problem is with respect to shear strength, it is applicable to both C and Φ.
Given that:
γ = 2.1 gm/c.c
Φ=15º,
C= 0.2 kg/cm2 = 20 KN/m2
F=2.5
we have,
F= tanΦ/ tanΦm
Φm= tan-1 (tan15º / 2.5)
Φm = 6.12º
For Φm = 6.12º and i = 70º from stability chart
Sn=0.17
Again, Sn= C / FγHc
Hc = 20 / 2.5 x 21x 0.17
Hc = 2.24 m
∴ Safe height of embankment = 2.24m
3. Find the factor of safety of a slope of infinite extent and made with clay having C = 30 kN/m2, Φ = 20º, e = 0.65, and G = 2.7 under the following conditions:
1. when the slope is dry
2. when the water seeps parallel to the surface of the slope.
3. when the slope is submerged.
Solution:
Given that:
C = 30 kN/m2
Φ = 20º
e = 0.65
G = 2.7
γsat = (G+e)γw / (1+e)
γsat = (2.7+0.65) x 10 / (1+0.65)
γsat = 20.30 KN/m3
Again,
γd = Gγw / (1+e)
γd = 2.7×10 / 1.65
γd = 16.36 KN/m3
Assume z= 5m and i= 30º
1. when the slope is dry
Fs = 52.33 / 35.42
Fs = 1.48
2. when the water seeps parallel to the surface of the slope.
Fs = 1.002
3. when the slope is submerged.
Fs = 1.98
4. A 5 m deep canal has side slopes of 1:1. The properties of soil are Cu= 20 KN/m3, Φ=10°, e = 0.8, and G = 2.8. If Taylor’s stability number is 0.108, determine the factor of safety with respect to cohesion, when the canal runs full. Also find the same in case of sudden drawdown, if Taylor’s stability number for this condition is 0.137.
Solution:
Given that:
Cu= 20 KN/m3
Φ=10°
e = 0.8
G = 2.8
γsat = (G+e)γw / (1+e)
γsat = (2.8+0.8)x9.81 / (1+0.8)
γsat = 19.62 KN/m3
Also,
γ’ = γsat – γw
γ’ = 19.62-9.81
γ’= 9.81 KN/m3
Case I: When canals run fully the side slopes are submerged.
Sn = C / (Fc γ’ H)
Fc = C / (Sn γ’ H)
Fc = 20 / (0.180 x 9.81 x 5)
Fc = 3.8
Case II: Sudden Drawdown Condition
Sn = 0.137
Here,
Fc = C / Sn γsat H
Fc = 20 / (0.137 x 19.62 x 5)
Fc = 1.5
| Read Also: Formation of Soils |

