Table of Contents
The slenderness ratio of a reinforced concrete (RC) column may be defined as the ratio between the length of the column, its lateral dimensions, and end fixity. It evaluates the capability of the reinforced concrete column to withstand buckling pressure.
The slenderness ratio is computed by dividing the column length by its radius of gyration.
The slenderness ratio differentiates a short column from a long or slender column. The design of the former is owned by column dimension and material strength whereas the latter is controlled by column slenderness.
Columns are defined as long slender member load axially in compression and having lateral dimensions very small as compared to their lengths.
A vertical compression member is called a column. If load passes through the longitudinal axis coinciding with CG of the column, it is called the axially loaded column, or otherwise eccentrically loaded column.
Columns are the building structures connected to different footings to transfer the load of the building to the footings of the buildings.
There are two types of columns: Slender columns and Short columns.
Slender columns are those columns whose cross-sectional dimensions are small compared to their length and this column was introduced with the finding of high strength materials.
Short columns are those columns whose cross-sectional dimensions are more compared to their length and this type of column is more widely used over slender columns.
Concrete columns, whether slender or short, uses main reinforcement parallel to the vertical loads and use rectangular or circular ties to prevent the bars from buckling action. While pouring concrete, the vertical reinforcement has to be erected straight.
A column is considered slender if its cross-sectional dimensions are small compared to its length. If the slenderness ratio of a column is high, it will crumple under a smaller compression load in contrast to a short column with the exact cross-sectional dimensions. So, the slenderness effect should be carried into consideration during the design process.
The slenderness ratio of reinforced concrete columns can be calculated according to the instructions and specifications of applicable codes such as ACI 318-19 and IS 456.
How to Calculate Slenderness Ratio Based on ACI 318-19?
The degree of slenderness is generally expressed in terms of the slenderness ratio:
| Slenderness Ratio (λ) = K lu / r |
where:
lu: unsupported length of the member
r: radius of gyration of its cross-section
K: constant to reflect end conditions of the column; distance between two inflection points (Alignment chart is used to calculate K).
Unsupported Length of the Member (lu)
The unsupported length (lu) of a column is measured as the clear distance between the underside of the beam, slab, or column capital above, and the top of the beam or slab below.

The unsupported length of a column may be different in two orthogonal directions depending on the supporting elements in respective directions.

Radius of Gyration of Column Cross-section (r)
The radius of gyration introduces the effects of cross-sectional size and shape on slenderness. For the same cross-sectional area, a section with a higher moment of inertia produces a more stable column with a lower slenderness ratio. The radius of gyration r is calculated using the following formula:
| r = √Ig/Ag |
Ig: a moment of inertia of gross concrete section about a centroidal axis, neglecting reinforcement, mm4
Ag: Gross area of the column, mm2
It is possible to use the approximations of r = 0.3h for square and rectangular sections, and r = 0.25h for circular sections.
where,
h: overall sectional dimension in the directional stability is being considered.

Effective Length Factor (k)
The effective length factor (k) reflects the end restraint (support) and lateral bracing conditions of a column. If a column is hinged at both ends, it follows a half-sine wave when it buckles, and the value of the (k) factor for such type of column is 1.0. So, the effective length of the column (klu) is equal to the unsupported length of the column (lu).
A column with fully restrained end conditions develops deflected shape as shown in Figure-5. The portion of the column between the points of contra flexure follows a half-sine wave. The effective length factor k for this case is equal to 0.5.

Columns in real structures are rarely either hinged or fixed but have ends partially restrained against rotation by abutting members. The value of k, in this case, varies between 0.5 and 1.0 for laterally braced columns, Figure-6. For unbraced columns, the value of k varies between 1.0 and ∞.
The majority of reinforced concrete columns are considered to be laterally braced columns. The exact value depends on the degree of end restraint, that is, on the ratio of the stiffness (EI/l) of the column to the sum of stiffnesses (EI/l) of the restraining members at both ends.


ACI Criteria for Slenderness Ratio Effect
The effect of the slenderness ratio for columns braced against sideway can be neglected when:
| (K lu / r) ≤ 34 + 12 (M1/M2) , and (K lu / r) ≤ 40 |
Note: As a first approximation, k may be taken equal to 1.0 in this equation
Where:
M1: lesser factored end moment on a compression member, N·mm
M2: greater factored end moment on a compression member.
M1/M2: negative if the column is bent in single curvature, and positive for double curvature. M1/M2 is negative if the column is bent in single curvature, and positive for double curvature:
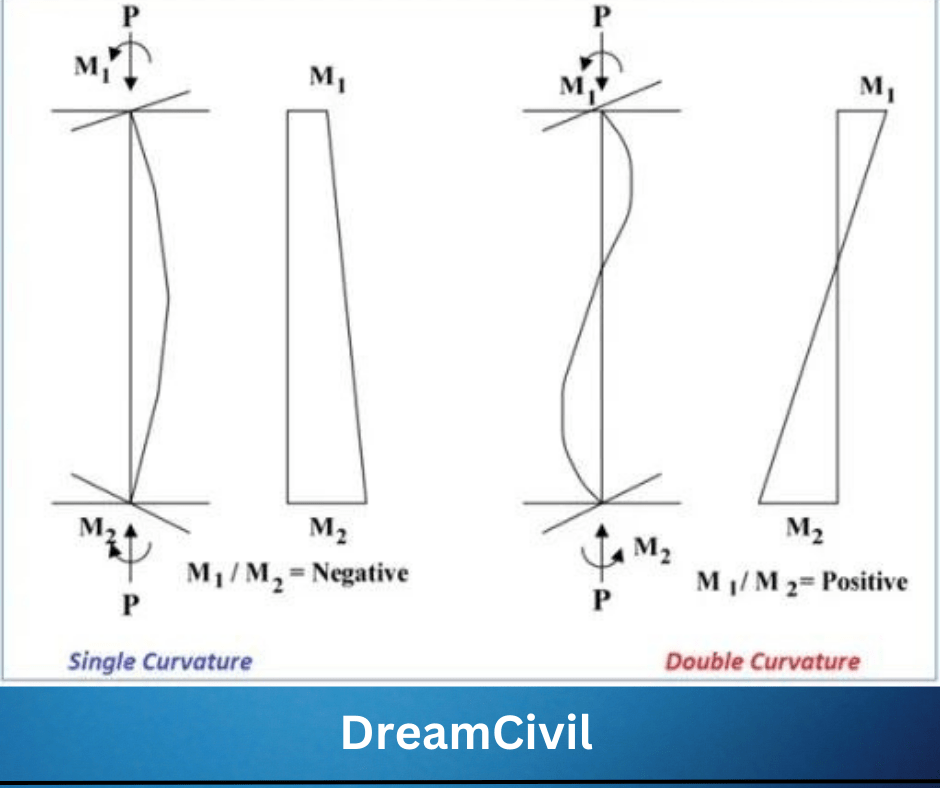
The effect of the slenderness ratio for columns not braced against sideway can be neglected when:
| (K lu / r) ≤ 22 |
Alignment Chart for Effective Slenderness Factor
If slenderness is seen to be essential, redefine the calculation of k relying on the alignment chart as shown below:
The Ψ factor at one end of the column is equivalent to the sum of the stiffness ∑(EI/L) of the columns encountering that joint, including the column in question, divided by the sum of all the stiffnesses of the beams encountering the joint.
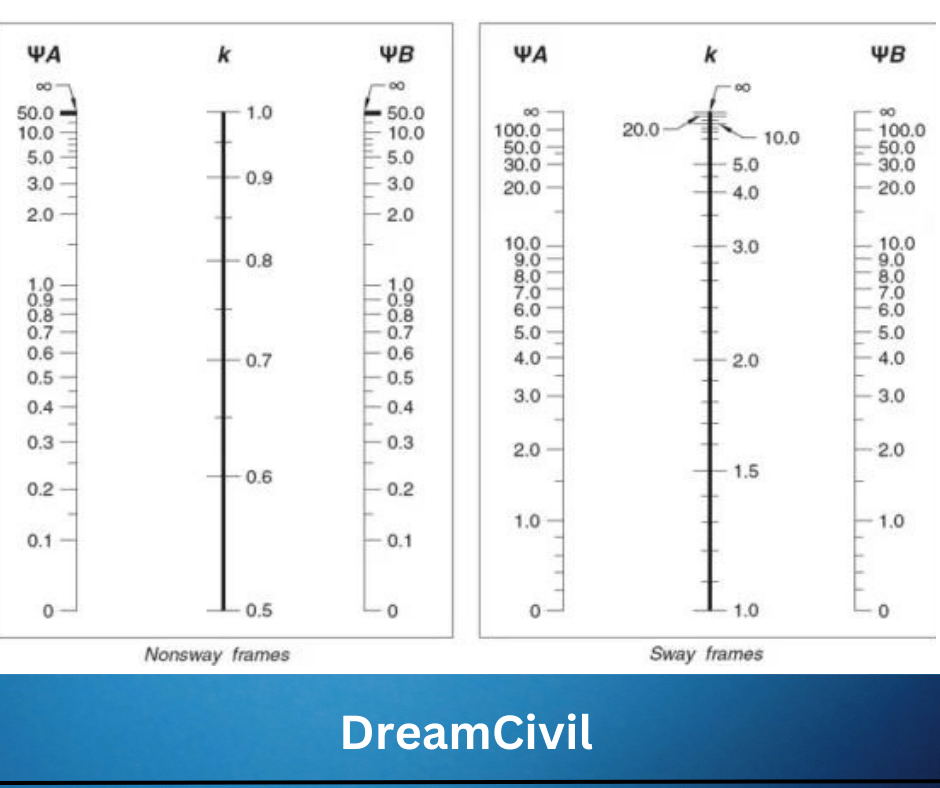
| Ψ = ∑(EI/L)c / ∑(EI/L)b |
Where:
E: Modulus of Elasticity
I: Moment of Inertia
L: span length measured center to center of joints.
ΨA, ΨB: Values of (Ψ ) at each end of the column
The modulus of elasticity for normal concrete is computed as:
| Ec = 4700√F’c |
The moment of inertia used to compute Ψshould be based on the cracked section, so ACI 318-19 section 6.6.3.1.1 provides Table-1:
| Member and Condition | Moment of Inertia |
| Columns | 0.70Ig |
| Uncracked walls | 0.70Ig |
| Cracked Walls | 0.35Ig |
| Beams | 0.35Ig |
| Flate Plates and Flat Slabs | 0.25Ig |
Table-1: Moment of Inertia Used to Compute Ψ Factor
FAQs
1. How do you decide if a column is short or slender?
The column is supposed to be slender if its length is increased compared to its cross-sectional dimension i.e. slenderness ratio is employed to differentiate a slender column from a short column.
3. What is the slenderness ratio of a reinforced concrete column?
The slenderness ratio of reinforced concrete (RC) column may bed defined as the ratio between column length, its lateral dimensions, and end fixity. It evaluates the ability of reinforced concrete columns to withstand buckling pressure.
4. What is the use of the slenderness ratio?
It is used to find out the design load as well as in classifying various columns in short/intermediate/long. The slenderness ratio of a column provides an expression of buckling failure in the column.
The more the slenderness ratio, the more the chance of the column failing by buckling
effect in that path.
5. How do you calculate the slenderness ratio of a column?
a. Compute the effective length factor (K) that is between 0.5 to 1.0 for the reinforced concrete column. It can be assumed to be 1.0 conservatively.
b. Compute the unsupported length of the column (lu) which is calculated as the clear distance between the underside of the beam, slab, or column capital above and the top of the beam or slab beneath.
c. Calculate the radius of gyration (r). It is attainable to employ the approximations of r = 0.3h for square and rectangular sections, and r = 0.25h for circular sections.
d. Calculate the slenderness ratio which is equivalent to the effective length factor times unsupported length divided by the radius of gyration.
6. What is the buckling of the column?
The buckling of the column is a condition of deformation as a result of axial compression forces that shows the bending of the column, as a result of the instability of the column. This mode of failure is temporary and unpleasant.
7. What is the radius of the gyration of the column?
The radius of Gyration may be used to define the distribution of cross-sectional area in a Reinforced concrete column around its centroidal axis.
Read Also: Mistakes to Avoid While Choosing a Plumber

