Table of Contents
In this article, we will discuss the degree of static indeterminacy
1. Introduction
There are lots of structures that can move concerning earth without deforming its natural system. Such ability of the system is termed as freedom of a system whose degree differs with the type of structure in the 2D and 3D planes.
To prevent the structure from failure, we need to know about the degree of freedom of the system and the degree of static indeterminacy.
In-plane, a body should be capable of translational and rotational motion to have a degree of freedom. The degree of freedom depends upon the type of support used and boundary conditions.
Mainly, there are two types of structures whose reactions and internal stresses developed in the plane member need to be determined. They are statically determinate and statically indeterminate.
The structure whose reactions and internal stresses can be determined directly by using three static equilibrium equations and conditional equations (internal hinge in structure), then the system is said to be statically determinate.
While the structure whose reactions components and internal stresses can’t be determined using those static equilibrium equations and conditional equations are termed as statically indeterminate.
Three static equilibrium equations are:
∑Fx =0, ∑Fy=0, ∑M=0
2. Objectives of The Degree of Static Indeterminacy
To know the structure is either statically determinate or statically indeterminate or unstable, we have to determine the degree of static indeterminacy.
The degree of static indeterminacy is defined as the number of additional equations required to determine the static unknowns in the structure.
The value of the degree of static indeterminacy depends upon the geometry (2D or 3D) of structures (frame or truss).
If the Degree of static indeterminacy (Ds) = 0, the structure is statically determinate.
If Ds<0, the structure is unstable.
If Ds>0, the structure is statically indeterminate.
Note: Beam has kinematic indeterminacy. A fixed beam is kinematic determinate while a simply supported beam is kinematic indeterminate.
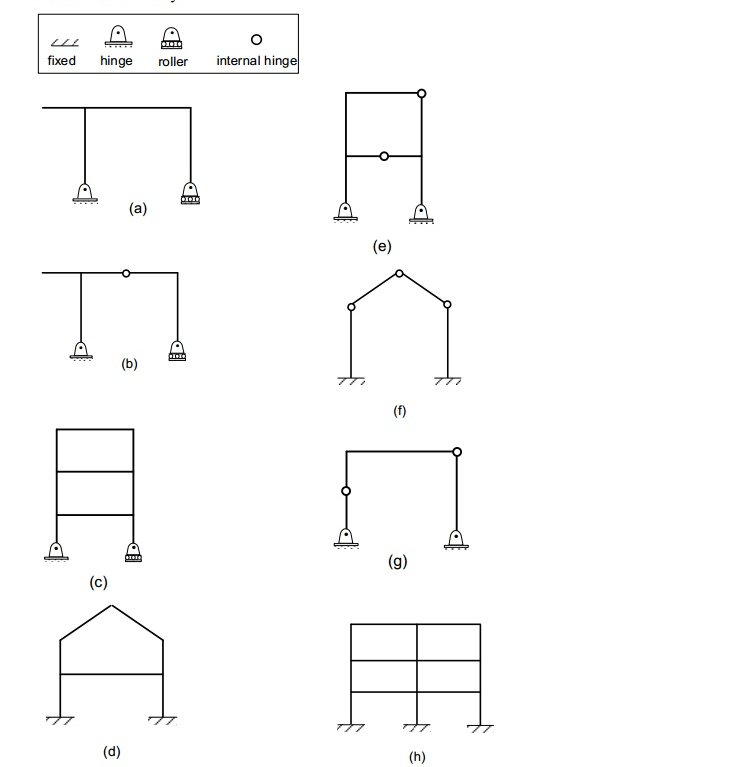
3. Determination of Degree of Static Indeterminacy
To determine the degree of static indeterminacy of any structures, we should know about the following terms:
a. Type of structure ( frame or truss either in 2D or 3D plane).
b. Number of supports(hinge, roller, fixed)and internal hinges present in the structure.
c. Number of restraints(restrictions to move freely in space connected to a stationary body I.e. static) of supports.
d. Mathematically,
The degree of static indeterminacy is the sum of the degree of internal static indeterminacy(Dsi) and the degree of external static indeterminacy (Dse).
i.e. Ds = Dsi + Dse
Here,
We have formulae for 2D and 3D Framed structures and Truss structures.
3.1. For the Degree of Internal Static Indeterminacy
a. It deals with the geometry stability of the structure.
b. It is the inability of structure to calculate the internal forces using static equilibrium equations.
c. Dsi = 3C (for 2D framed Structure)
d. Dsi = 6C (for 3D framed structure) Where C is the no. of a closed surface.
e. If Internal hinges are provided then Dsi=3C – ∑(n-1) for 2D framed structure.
f. If Internal hinges are provided then Dse = 6C-∑3(n-1) for 3D framed structure.
g. Dsi = m-(2j-3) for truss structure where m is the no. of members, j is the no of Joints.
3.2. For Degree of External Static Indeterminacy
a. It deals with the support condition.
b. It is the inability of structure to determine all the external forces using supports reactions.
c. Dse = r-3 (for framed 2D structure and Truss).
d. Dse = r-6 (for 3D structure and truss) Where r is the no. of restraints of supports.
| Read More: Building Substructure |
| Read More: Structure Relocation |
